Table of Contents
In our article about Basic Linear Functions, we learned that the equation y = mx + b can be used. to represent linear functions in the 2D coordinate plane. In this article, we will dive a little deeper and learn two new equations.
Mystery of Geometry
one to calculate the slope of any line, and the other to calculate the distance between two points on a line. To do that, the first thing we need is two points. Yes! Two points !! Actually, I mean two points on the coordinate plane, but the shot is good.
We will name these points “Point 1” and “Point 2”. As you know from Geometry, a line can be determined by two points. All you need to do is “connect the dots” to get the line segments. And you can get unlimited lines by expanding the line segment in any direction.
Our goal in this article is to learn how to find the slope of a line segment like this. and to calculate the distance between two end points. The key to achieving this goal is to realize that you can use any line segment to make a right triangle.
To do that, start from the highest point in the coordinate plane. and draw a straight vertical line down to the bottom of the coordinate plane.
Next, move to another point and draw a horizontal line until it intersects the vertical line that you just drew. See now you have a right triangle. The vertical and horizontal sides of the right triangle. perpendicular to each other so that they form the correct angle.
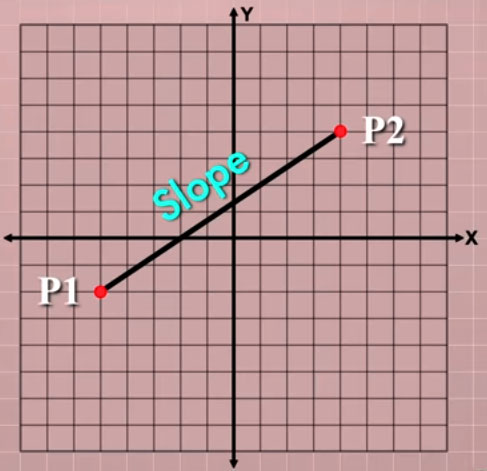
And the original diagonal line segment is now the hypotenuse of the new triangle. For the time being, we will call the horizontal side of the triangle “changing x”. and the vertical side “changes in y”, which is an awkward long name, but that’s what the two sides represent. Imagine starting from Point 1 and then slowly moving along our line segment towards Point 2.
When you do that, the X and Y coordinates in your place change, right? Your X coordinates change because you travel right, and your Y coordinates change because you travel. And when you finally get to Point 2, the total change in your X coordinates will be the length of the horizontal side of the triangle, and the total change in your Y coordinate will be the length of the vertical side of the triangle.
That’s cool, but the names “change X” and “change Y” are rather long. Fortunately, mathematicians have a shorter way to say the same thing. They use the Greek letter “delta” as an abbreviation for the word “change”.

That means you can write or say “delta X” which means “change X”. and “delta Y” means “change Y”. OK, now we know what those parties represent and we have good names for them, how do we actually calculate the lengths of the sides? To do that, we only need the coordinates of the two points that make up our line. Because we named it Point 1 and Point 2, it made sense to us.
to call their coordinate values ”X1 and Y1″ for Point 1 and “X2 and Y2” for Point 2. We write 1s and 2s as subscripts after the variable. so we don’t wrongly think it means X times 1 or X times 2. The subscript numbers are just a way to distinguish different variables in the problem. so we can track which one. However, to calculate (delta X), you need to find the difference between the X coordinates of two points.
Algebraic Formulae
In other words, you need to subtract X from the first point from X from the second point. So (delta X) = X2 – X1. Likewise, to calculate (delta Y), you need to find the difference between the Y coordinates of two points. So (delta Y) = Y2 – Y1.
This simple equation for finding (delta X) and (delta Y) is important. because they are used in equations for slope and distance, which I want to show you now. The equation for the slope of the line looks like this.
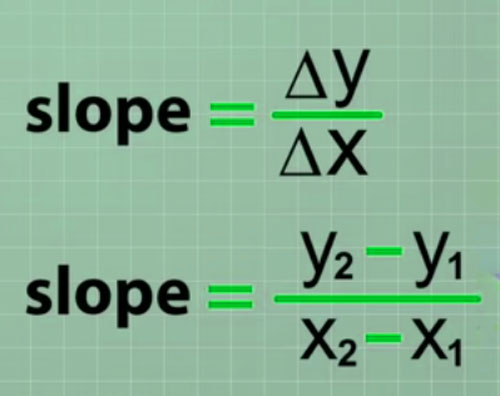
The only difference is that (delta X) and (delta Y) have been written. to show the reduction you need to do to get these values from coordinates. Whatever way you want to write it is fine. And some of you may have heard this same equation expressed using different terminology.
Have you ever heard someone say “slope = rise over run” ?. “Up” and “Running” are just different names that are sometimes used to describe changes in Y and changes in X. The idea is that if you “run” along the line in the X direction, you will “go up” by the number certain when you do that. Or will you. What if the line has a negative slope?
which means that when you move in the positive X direction, the value of Y decreases instead of increasing ?. It would be like going downhill instead of going up and the word “up” doesn’t seem right in that case.
Therefore, we will only use (delta Y) above (delta X) in this article. But of course it’s not wrong to use the terms “rise” and “run”, especially if it helps you remember the formula.
But if you do, just remember that “awakening” can also be negative. Now that you have seen the equation for slope, let’s look at the equation for calculating the distance between two points on the line. The distance is equal to the square root of [(delta X) squared plus (delta Y) squared]. Hmmm does this equation remind you of something you might have seen before?
It certainly reminds me of something I’ve seen before! You stole my theorem !. Ah Um Hai, there is Pythagoras. I did not steal your theorem. I only borrowed it so that I could count a few items. Don’t worry, I’ll give you credit for that.
I guess as long as you give me credit. Do you remember how the Pythagorean Theorem tells us the relationship between the three sides of a right triangle ?. That means that if you know the length of the two sides, you can calculate the length of the third side.
Well, we have just seen that if you convert a line segment to a right triangle, you can calculate the length of the two sides which will become (delta X) and (delta Y), right?
So we can incorporate those values into The Pythagorean Theorem. You are accustomed to seeing theorems in this form: ‘a squared’ + ‘b squared’ = ‘c squared’. Because ‘a’ and ‘b’ are horizontal and vertical side lengths, we can plug (delta X) and (delta Y) instead. And instead of ‘c squared’ for the hypotenuse, let’s use ‘d squared’. because the length of the hypotenuse is equal to the “distance” between our two points. To solve ‘d’ (or distance), we take the square root from both sides and we get. d = square root of [(delta X) squared + (delta Y) squared].
Pythagoras Conference Global
This particular form of the Pythagoras Theorem is usually called the “Distance Formula” in Algebra. because you can use it to find the distance between two points in the coordinate plane. And as is the case with Slope Equation, you will often see it in an expanded form. where (delta X) and (delta Y) are written as subtractions X2 – X1 and Y2 – Y1.
Alright, now that we have an equation for slope and distance, let’s see them in action. Suppose we are given two coordinates and we are asked to find the slope of the lines they form, and the distance between these points in the coordinate plane.
The first thing we need to do is name the coordinates because they haven’t been named. And even though it’s not really necessary, if you’re like me, you might want to draw a small sketch of the problem to help you visualize what’s happening. The equations for slope and distance are both used (delta X) and (delta Y). so let’s calculate the values first. (delta X) = X2 – X1, and in this problem, X2 = 4 and X1 = -2. So (delta X) is equal to 4 minus -2 which is only 6. Next we count (delta Y). (delta Y) = Y2 – Y1. and in this problem, Y2 = 3 and Y1 = 0. That means (delta Y) = 3 minus 0 which is only 3.
Great, now we have our (delta X) and (delta Y) values. and you can confirm that we got it right by looking at our chart. The side length (delta X) is 6 units, and the side length (delta Y) is 3 units. Now let’s attach the delta values to the equation for slope and distance. Slope = (delta Y) more than (delta X). We have just found that (delta Y) = 3 and (delta X) = 6, so our slope is equal to 3 over 6, which simplifies to half or 0.5. That’s easy, now let’s plug the deltas into our Equation Distance to see how far apart those points are. Doing so tells us that distance = square root of (‘6 squared’ + ‘3 squared’).
‘6 squared’ = 36 and ‘3 squared’ = 9. 36 + 9 = 45, so the distance between points will be the square root of 45. You can also simplify the answer for ‘3 root 5’. or use a calculator to convert it to decimal which will be 6,708 (rounded up to 3 places). That’s not too bad, is it? But let’s try one more example to make sure you get it.
Once again, we are given two points, but this time they have been shown on the coordinate plane for us. We will label this one farthest to the left, Point 1 and the other Point 2. That means the coordinates of this point are X1 and Y1. and the coordinates of this point are X2 and Y2. First, we attach the coordinate value to the delta equation. (delta X) = X2 – X1 which is 1 minus -3.
Algebra Basic
So (delta X) = 4. (delta Y) = Y2 – Y1 which is -2 minus 5. So (delta Y) = -7. Once again, we see that the delta values are in accordance with the graph. and a right triangle formed by a line between two points.
Or are they? One of our deltas is negative, but the length cannot be negative, right? Yes no, but remember that deltas really are the difference between coordinate values, so they can be negative.
The length of the sides of a triangle is really the Absolute Value of a delta. But delta signs are important because they help us get the right slope, because the slope can be positive or negative. Now that we have our delta, let’s plug it into the equation for the slope. The slope = (delta Y) is more than (delta X) which will be -7 more than 4.
We can leave such slopes as incorrect parts. But we can also convert it to a mixed number form, or get a decimal value with a calculator, which is -1.75. Now that we have found the slope, let’s find the distance between the points by entering the delta that we have calculated into the equation. That gives us distance = square root of (‘4 squared’ + ‘negative 7 squared’).
‘4 squared’ = 16 and ‘negative 7 squared’ = 49. That means distance is the square root of (16 + 49) or square root of 65. The root cannot be simplified, but we can use a calculator to convert it to decimal if we want, give us a distance of 8062 (rounded up to three decimal places).
Alright, so now you know how to calculate the slope of a line if you know two points along that line.
You also know how to calculate the distance between two points on a line using the so-called Distance Formula. Also known as the Pythagorean Theorem, discovered by ME, Pythagorean. Ah yes, thank you for reminding us of Pythagoras.
Remember that the key to success in mathematics is practice, so be sure to try some of your own slope and distance problems. Learn more at www.pythagorasconferenceglobal.com.

